[KR] Continual Post-Training of LLMs via Offline GRPO for Mathematical Reasoning
이 포스팅에서는 거대 언어 모델(LLM)의 추론 능력을 지속적인 추가 학습(Continual Post-training)을 통해 향상시키는 새로운 접근법을 소개합니다. 기존의 사전 학습(Pre-training)은 광범위한 언어적 지식을 제공하지만, 수학이나 코드 생성과 같은 복잡한 추론 작업에서는 여전히 한계를 드러냅니다. 최근 연구에서는 강화학습 기반의 검증 가능한 보상 기법(RLVR)이 이러한 한계를 어느 정도 해소할 수 있다고 밝혔으나, 현재까지 제안된 방법들은 느리고 제한적인 온라인 (Online) 학습에 의존하고 있습니다. 우리는 이 문제를 해결하기 위해 교사 모델이 생성한 우수한 추론 경로(Trajectory)만을 활용하는 오프라인 (Offline) 학습 방식을 제안하며, 특히 모든 생성된 결과가 긍정적인 경우에도 고품질의 추론 과정을 효과적으로 학습할 수 있도록 GRPO 알고리즘의 새로운 변형 방식을 도입했습니다. 수학적 추론을 대상으로 한 실험 결과, 제안한 방법이 일관된 성능 향상을 보임을 확인하였으며, 학습된 모든 모델의 checkpoint와 학습 코드를 공개하였습니다.
Boosting Math Reasoning in Open-Source LLMs
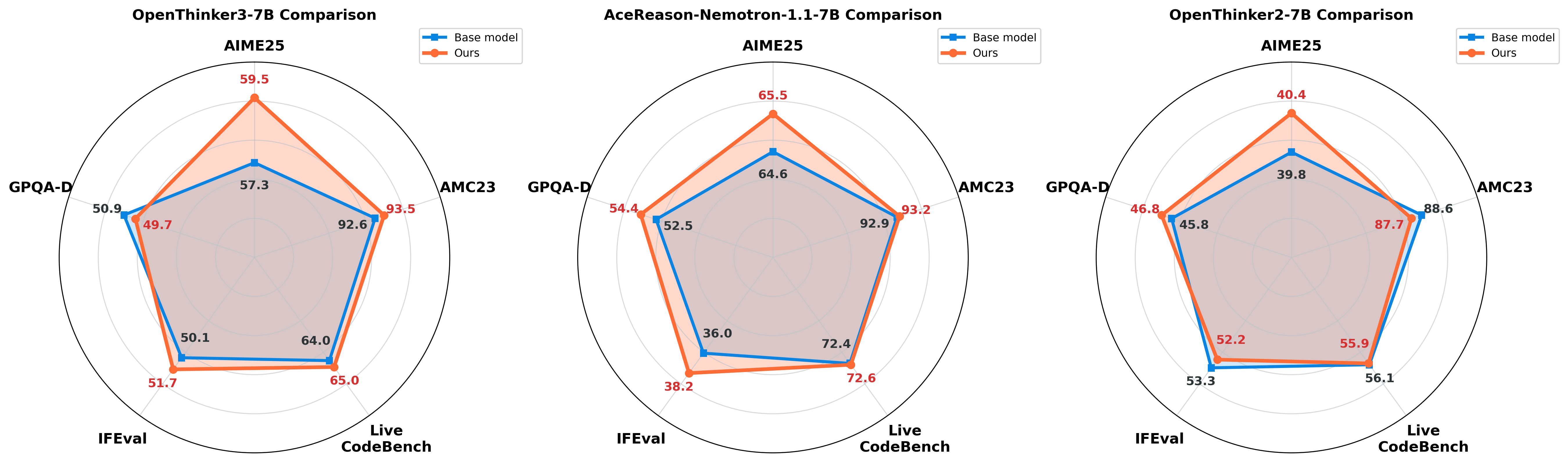
우리는 여러 추론형 Large Language Models (LLMs) 들의 수학 추론 성능을 더 끌어올리 위해 활용할 수 있는 continual post-training 방법을 제안했습니다. 기존에 많이 활용되는 on-policy GRPO는 매 step마다 model에서 rollout을 통해 sample을 뽑아야 하기 때문에 rollout 과정에서 많은 시간이 소요될 뿐 아니라, 학습 초기의 base LLM 성능이 좋지 않을 경우 높은 reward를 갖는 좋은 sample 자체를 거의 얻을 수 없다는 문제가 있습니다. 이러한 단점을 해결하기 위해, 미리 준비해둔 teacher의 reasoning trajectory만을 활용하여 offline GRPO를 진행합니다. 추가적으로, 기존 GRPO는 group 내 모든 sample이 positive일 경우 advantage가 0이 되어 학습이 이루어지지 않는데, 여기선 teacher가 생성한 trajectory만을 다룸으로 모두 positive이더라도 supervision을 받을 수 있도록 GRPO의 advantage에 bias term을 추가하는 방식을 제안합니다. 최종적으로, Figure 1 과 같이 수학에 더 특화된 성능을 얻은 LLM들을 얻을 수 있었습니다. 또한, 이 학습 방법으로 수학이 아닌 다른 task에서는 기존 모델과 유사한 성능을 유지할 수 있음을 확인했습니다.
Why do we focus on post-training for reasoning?
Large text corpus로 학습하는 LLM의 사전학습(pre‑training)은 언어의 통계적 패턴과 구조를 이해하는 데 큰 역할을 합니다. 하지만 단계를 거쳐야 하는 복잡한 논리 추론, 수학적 문제 해결, 또는 코드 작성과 같은 작업에서는 충분하지 않습니다. 예컨대 Chain-of-Thought (CoT)를 쓰면 어느 정도 추론 과정을 모방하게 할 수 있지만, 이는 모델이 일관된 사고 흐름을 자기 것으로 내재화한 것이 아니라 성능의 한계가 존재합니다.
이런 한계를 극복하기 위한 post-training 방법 중 하나로 Reinforcement Learning with Verifiable Rewards (RLVR) 이 있습니다. 이 방식의 post-training이 LLM의 추론 강화에 효과적이라는 사실은 DeepSeek-R1 이나 OpenAI의 o1/o3 모델과 같은 모델들이 RLVR 방식을 통해 실질적인 추론 성능향상을 보이면서 더 각광을 받게 되었습니다. RLVR은 LLM이 생성한 전체 추론 과정인 chain-of-thought(CoT) 형태의 rollout trajectory가 검증 가능해야 합니다. 예를 들어, 수학 문제의 정답이 있어서 최종 정답이 비교가 되거나, 각 단계에 대한 평가가 가능해, 생성된 rollout trajectory 전체에 대해 보상(reward)을 줄 수 있는 구조입니다. 이런 보상을 바탕으로, RL 알고리즘(e.g., PPO, GRPO)을 통해, LLM은 검증된 추론 과정을 더 많이 생성하도록 학습되게 됩니다.
대표적인 RLVR 방식의 학습 알고리즘으로는 Group Relative Policy Optimization (GRPO) 방식
여기서, $\pi^{i,t} = \pi(o_{i,t}\mid q, o_{i,<t})$이며, $G$는 한 그룹 내 응답 개수를 의미합니다. 또한, $\pi_\text{ref}$, $\pi_{\theta}$, $\pi_\text{old}$는 각각 기준(reference) LLM, 학습 중인 LLM, 샘플링에 사용되는 LLM을 나타냅니다. $q$와 ${o_i}_{i=1}^{G}$는 학습에 사용되는 질문과 생성된 rollout trajectory 세트를 나타냅니다. 각 응답의 상대적 advantage인 $\hat{A}_i$는 다음과 같이 계산됩니다.
\[\hat{A}_i = \frac{r_i - \text{mean}(r_i)}{\text{std}(r_i)}\]이렇게 계산된 trajectory level 의 advantage는 응답의 각 토큰 수준에 적용되어 최종적으로 $\hat{A}_{i,t}$로 사용됩니다.
Offline Reinforcement Learning with Verifiable Reward
Why do we focus on Offline RLVR (e.g., GRPO)?
앞서 설명한 RLVR 의 경우는 on-policy 로 advantage를 업데이트 하는 방식입니다. On-policy 의 경우, 학습하는 모델이 뽑아낸 roll-out trajectory 에 대해 reward 를 계산해 이를 통해 LLM을 업데이트 한다는 것을 의미합니다.
하지만, on-policy로 학습하는 것에는 두가지 단점이 존재합니다.
첫번째 단점은 학습 속도가 매우 느리다는 것입니다.
On-policy 의 문제들을 해결하기 위해, 저희는 정답 label 을 뽑기 위해 쓴 teacher LLM의 roll-out trajectory 를 활용하는 offline RLVR 방식을 도입했습니다.
저희가 이번 프로젝트에 활용한 데이터는 OpenThought3
이 때, Teacher model 을 $\theta_\text{teacher}$ 라고 하고, teacher가 정답 label을 뽑기 위해 roll-out 한 문제들의 random variable을 $Q$ 라고 할 때, 우리는 offline GRPO를 아래와 같이 수식을 쓸 수 있습니다:
\[\mathcal{L}_{Off-GRPO}(\theta) = \mathbb{E}_{[q \sim P(Q), \{o_i\}_{i=1}^{G}\sim \pi_{\theta_\text{teacher}}(O|q)]}\left[ \frac{1}{G}\sum_{i=1}^{G}\frac{1}{|o_i|}\sum_{t=1}^{|o_i|}\left\{ \min\left[\frac{\pi_{\theta}^{i,t}}{\pi_{\theta_\text{teacher}}^{i,t}}\hat{A}_{i,t},\text{clip}\left(\frac{\pi_{\theta}^{i,t}}{\pi_{\theta_\text{teacher}}^{i,t}},1-\epsilon,1+\epsilon\right)\hat{A}_{i,t}\right] -\beta\mathbb{D}_{KL}\left[\pi_{\theta}\mid\mid\pi_\text{ref}\right]\right\} \right]\]이 때, practical 하게 teacher 의 probability 를 모르기 때문에, $\pi_{\theta_\text{teacher}}^{i,t}=1$ 로 가정하였습니다.
그러면 항상 $\frac{\pi_{\theta}^{i,t}}{\pi_{\theta_\text{teacher}}^{i,t}} \le 1$ 이기 때문에, $\text{clip}$ 은 $\max\left(\pi_{\theta}^{i,t},1-\epsilon\right)$ 로 표현될 수 있습니다.
최종적으로, practical하게 offline 에 해당하는 GRPO 수식은 아래와 같이 근사될 수 있습니다.
Offline GRPO vs. Supervised Fine-tuning (SFT)
제일 간단하게 offline으로 준비된 teacher sample 로 학습한다는 것은 SFT를 하는 것으로 생각할 수 있습니다. 그러면 SFT 와 Offline GRPO 는 무슨 차이가 있을까요? 아래의 표현된 SFT 수식과 offline GRPO 의 수식을 비교하면 그 차이를 알 수 있습니다.
\[\mathcal{L}_{SFT}(\theta) = \mathbb{E}_{q \sim P(Q),\,o \sim \pi_{\theta_\text{teacher}}^{(+)}(O|q)}\left[\frac{1}{|o|}\sum_{t=1}^{|o|}\log\pi_{\theta}(o_{t}|q,o_{\lt t}) - \beta\mathbb{D}_{KL}\left[\pi_{\theta}\mid\mid\pi_\text{ref}\right]\right]\]여기서, $\pi_{\theta_\text{teacher}}^{(+)}(O|q)$는 teacher가 생성한 샘플 중에서 positive reward를 갖는 샘플만 선택했음을 나타냅니다. 이를 통해 모델은 오로지 positive 샘플의 분포를 따라가도록 지도학습을 수행하게 됩니다.
Practical하게 근사한 offline GRPO 수식과 비교했을 때, 우리의 Offline GRPO 수식은 negative 에 해당하는 sample 또한 반영된다는 점입니다. Offline GRPO 에서는 positive 와는 계속 가까워지게 학습을 하며, 반대로 negative 와는 멀어지게 학습을 하는 구조가 됩니다. 이로 인해 논리적으로 틀려 가지 않아야 할 rollout trajectory 에 멀어지게 되어, 더 추론 능력이 강화될 수 있습니다. 이 사실을 아래 실험을 통해 확인해 보았습니다.
Let’s try out our experiment
우리는 offline GRPO 방식이 단순히 positive 샘플만을 학습하는 supervised fine-tuning (SFT) 방식보다 추론 능력 강화에 더 효과적인지 확인하기 위해 실험을 수행했습니다. 실험에 사용된 모델은 OpenThinker3-7B이며, 데이터는 OpenThought3의 Math 문제 중 약 2,000개를 sampling하여 구성했습니다. 실험 환경은 VERL 프레임워크를 기반으로 구축되었고, 학습 과정에서 learning rate는 1e-7, batch size는 32, epoch는 3, KL coefficient는 0.1로 설정했습니다. 이때 각 문제당 8개의 샘플을 사용하여 학습을 진행했습니다.
성능 평가는 AIME24를 validation set으로 사용하여 각 epoch마다 성능을 측정했고, 3 epoch 중 가장 우수한 성능을 보인 checkpoint를 선정하여 최종적으로 AIME25-1과 AIME25-2에서 성능을 비교했습니다. 실험 결과는 다음과 같습니다.
| Method | AIME25-1 Score | AIME25-2 Score |
|---|---|---|
| Base model | 55.31 | 61.25 |
| SFT | 55.83 | 57.40 |
| Offline GRPO | 55.21 | 63.02 |
Offline GRPO 방식이 SFT보다 종합적으로 더 뛰어난 성능을 보인 이유는 negative sample들로부터 모델이 적극적으로 멀어지도록 학습을 유도했기 때문입니다. 기존의 데이터는 모두 positive sample로 고려되고 있지만, 본 실험에서는 majority voting과 Offline GRPO를 통해 보다 정확한 정보를 확보하고 이를 바탕으로 negative sample로부터 벗어나도록 유도하여, 더욱 세밀한 지도학습이 가능했습니다.
본 실험을 통해 Offline GRPO 방식이 기존 SOTA LLM의 논리적 추론 능력을 한 단계 더 향상시키는 데 매우 효과적임을 입증했습니다. 이 방식은 향후 다양한 추론 도메인에서도 충분히 적용 가능할 것으로 기대됩니다.
Proposed Loss for RLVR: Challenges & Solutions
Challenges: Considering all positive reasoning trace
Offline GRPO 는 그럼 문제가 없을까요? 아닙니다. 이유는 roll-out trajectory 가 all positive인 sample의 Advantage 값에 있습니다. 실제로 어떤 quesiton에 대해서는 전부 다 positive 인 sample 이 존재 할 수 있습니다. 이런 데이터의 경우 advantage 값을 계산하게 되면 mean reward 가 1 이 되어 0이 되고, 그러면 그 sample 들에 대해서는 update 가 되지 않습니다.
On-policy 의 경우에서는 이런 all positive sample 들이 부분이 문제가 안됩니다. 왜냐하면 이미 모델이 잘하는 경우라 update 를 하지 않아도 되기 때문입니다.
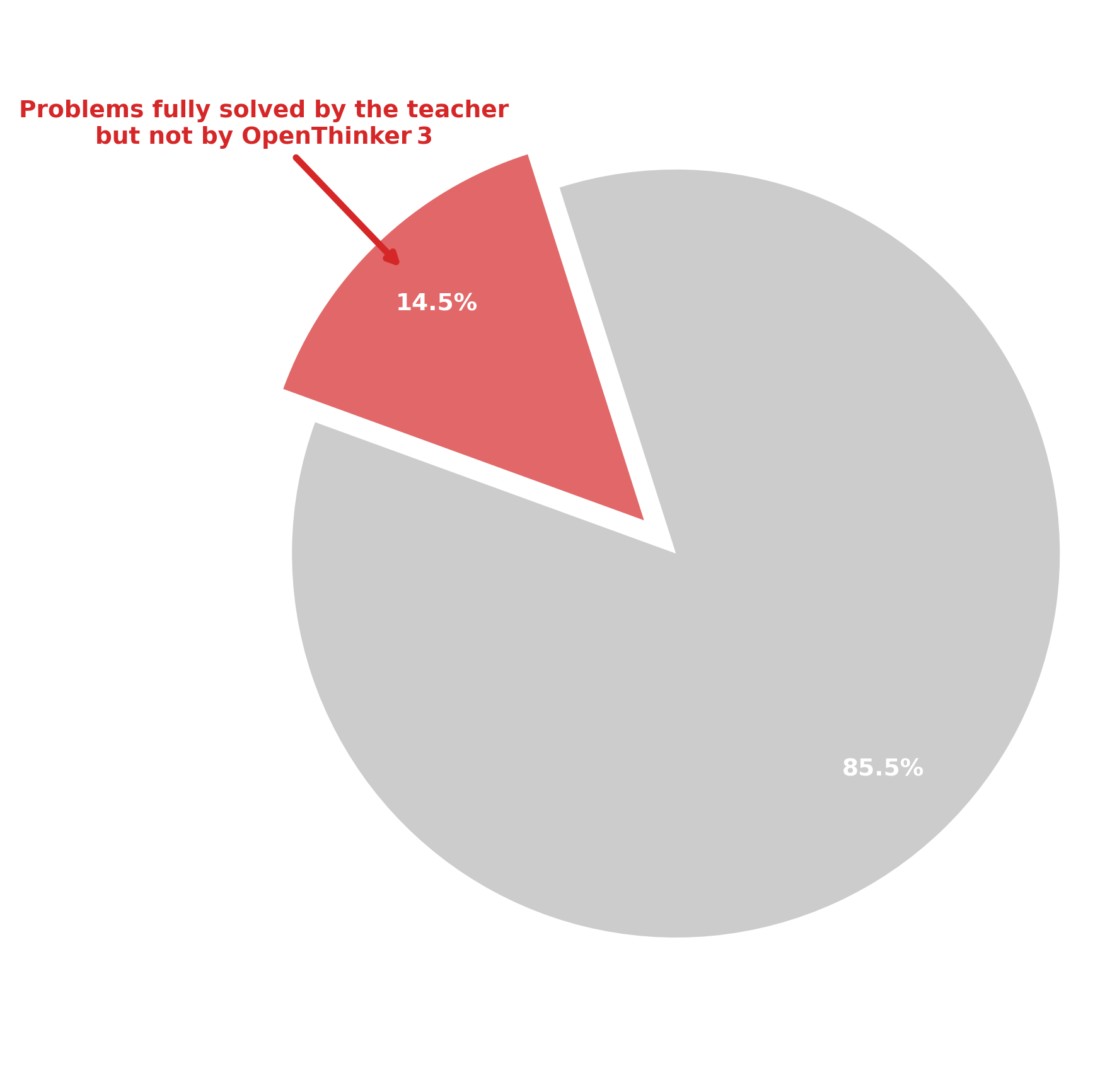
하지만, 반대로 Offline 의 경우에는 all positive sample 들을 학습하지 않는 것이 도움이 되지 않는 경우가 있습니다. Offline으로 준비한 sample 이 teacher sample 인 저희의 case 의 경우를 생각해 보겠습니다. 이 경우, teacher sample 은 전부 다 positive 여서 reward 가 1이지만, 실제 그 문제에 대해 저희가 학습할 target 모델은 틀린 sample 을 생성할 가능성이 높을 수 있습니다. 하지만 현재 Objective 로는 이 부분을 고려하지 못하고, 결국 배워야 할 rollout trajectory 에 대해 학습하지 못함을 의미합니다.
저희가 준비한 데이터에서 이 문제가 있음을 아래 그림을 통해 확인이 되었습니다.
Proposed method
위 문제를 해결하기 위해, 저희는 all positive roll-out trajectory 인 경우에는 advantage 에 bias term 인 $b$를 추가하는 simple 한 변형 loss term 을 제안하였습니다. 제안 방식을 통해 all positive 인 sample 이 나올 때도 그 sample 들에 대해 update 가 되도록 해주어서, all positive reasoning trace를 반영하지 못하는 문제를 해결합니다. 자세한 수식은 아래와 같습니다.
\[\mathcal{L}_{ours}(\theta) = \begin{cases} \mathbb{E}\left[ \frac{1}{G} \sum\limits_{i=1}^{G} \frac{1}{|o_i|} \sum\limits_{t=1}^{|o_i|} \left\{ \min\left[\pi_{\theta}^{i,t}(\hat{A}_{i,t} + b), \max(\pi_{\theta}^{i,t}, 1-\epsilon)(\hat{A}_{i,t} + b)\right] - \beta \mathbb{D}_{KL}\left[\pi_{\theta} \,\|\, \pi_\text{ref} \right] \right\} \right] & \text{if all } r_{i} > 0 \\ \\ \mathbb{E}\left[ \frac{1}{G} \sum\limits_{i=1}^{G} \frac{1}{|o_i|} \sum\limits_{t=1}^{|o_i|} \left\{ \min\left[\pi_{\theta}^{i,t} \hat{A}_{i,t}, \max(\pi_{\theta}^{i,t}, 1-\epsilon)\hat{A}_{i,t}\right] - \beta \mathbb{D}_{KL}\left[\pi_{\theta} \,\|\, \pi_\text{ref} \right] \right\} \right] & \text{otherwise} \end{cases}\]저희는 $b=0.1$ 로 setting 을 하고 실험을 진행했습니다.
Let’s try out our experiment
본 실험에서는 제안한 방식이 기존 offline GRPO보다 성능 향상에 도움이 되는지 추가로 검증하고자 하였습니다.
실험 환경은 첫 번째 실험과 완벽히 동일하며, 오직 학습 objective만 달라졌습니다. 동일한 모델(OpenThinker3-7B), 동일한 데이터(OpenThought3 Math 문제 2,000개), 동일한 hyperparameter(learning rate=1e-7, batch size=32, epoch=3, KL coefficient=0.1, 각 문제당 8개의 샘플)를 사용했습니다. 또한 bias term은 0.1로 설정하여 진행했습니다.
성능 평가는 동일한 방식으로 AIME24를 validation set으로 사용하여 best checkpoint를 선정한 후, 최종적으로 AIME25-1과 AIME25-2를 통해 성능을 평가했습니다. 실험 결과는 다음과 같습니다.
| Method | AIME25-1 Score | AIME25-2 Score |
|---|---|---|
| Base model | 55.31 | 61.25 |
| Offline GRPO | 55.21 | 63.02 |
| Offline GRPO (with all positive group bias) | 56.35 | 63.85 |
실험 결과, 제안한 modified offline GRPO 방식이 base model 뿐만 아니라 기존 offline GRPO 방식보다도 더 높은 성능을 기록했습니다. 이는 앞서 언급된 바와 같이, 기존 offline GRPO 방식에 더해 all positive sample 들까지 학습했기 때문으로 추측됩니다.
종합적으로, 제안한 modified loss 방식이 기존 offline GRPO의 한계였던 all-positive 샘플의 학습 문제를 성공적으로 극복했으며, 이를 통해 추론 성능을 더욱 강화할 수 있음을 확인했습니다. 향후 다른 다양한 추론 도메인에서도 이 방법론이 효과적으로 활용될 가능성이 클 것으로 기대됩니다.
Generalization Across Multiple Models and Benchmarks
우리는 제안한 continual post-training 방법론이 더 광범위한 모델과 다양한 벤치마크에서도 일관된 성능 개선을 보이는지 추가적으로 확인해 보았습니다. 이를 위해, 추가적으로 두 가지 모델(Openthinker2-7B, AceReason-Nemetron-1.1-7B)을 사용해 평가했습니다. 또한 평가를 위해 선택한 벤치마크는 수학 문제 해결 능력을 평가하는 AIME25와 AMC23, 코드 생성 능력을 평가하는 LiveCodeBench, 일반적 추론 능력을 평가하는 GPQA-Diamond, 그리고 사실 검증 성능을 평가하는 IFEval입니다. 여기서 AIME25와 AMC23, LiveCodeBench, GPQA-Diamond 평가에는 SkyThought framework, IFEval 평가엔 llm-evaluation-harness framework을 사용하였습니다.
실험 결과는 아래 표와 같습니다.
| Model | Method | AIME25 | AMC23 | LiveCodeBench | GPQA-Diamond | IFEval |
|---|---|---|---|---|---|---|
| Openthinker3-7B | Base | 57.292 | 92.617 | 63.968 | 50.947 | 50.09 |
| Offline GRPO (+bias) | 59.532 | 93.516 | 65.435 | 50.947 | 51.14 | |
| Openthinker2-7B | Base | 39.792 | 88.633 | 56.115 | 45.833 | 53.30 |
| Offline GRPO (+bias) | 40.573 | 88.359 | 56.115 | 46.717 | 52.62 | |
| AceReason-Nemetron-1.1-7B | Base | 64.635 | 92.930 | 72.383 | 52.462 | 36.02 |
| Offline GRPO (+bias) | 65.573 | 93.203 | 71.673 | 52.146 | 37.38 |
실험 결과를 통해 Math 데이터로 post-training한 만큼 수학 관련 벤치마크(AIME25, AMC23)에서는 모든 모델에서 일관된 성능 향상이 관찰되었습니다. 흥미롭게도, 다른 도메인에서의 성능 또한 기존 대비 저하되지 않고 유지되었으며, 특히 코드 생성 벤치마크인 LiveCodeBench에서는 오히려 소폭의 성능 향상이 관찰되었습니다. 이는 continual post-training 과정에서도 catastrophic forgetting이 거의 발생하지 않았다는 것을 의미합니다.
추가적으로, offline GRPO 방식은 실제 학습 과정에서 직접적인 rollout 없이 teacher model의 trajectory를 재활용하기 때문에 매우 효율적입니다. 이러한 효율성 덕분에 기존의 reinforcement learning 방식 대비 계산 자원을 현저히 절약하면서도, 성능은 동등하거나 더 뛰어난 결과를 달성했습니다. 따라서 저희가 제안한 continual post-training 방법론은 성능과 효율성을 모두 갖춘 실용적인 접근법으로, 향후 다양한 도메인과 응용 분야에서도 매우 유용하게 활용될 수 있을 것으로 기대합니다. 마지막으로, 오픈 소스 커뮤니티에 기여하고 연구의 재현성과 확장 가능성을 높이기 위해 HuggingFace와 GitHub에 평가한 모델들과 학습 코드 모두를 공개하였습니다.