[EN] Continual Post-Training of LLMs via Offline GRPO for Mathematical Reasoning
In this post, we explore a new approach to enhancing the reasoning capabilities of LLMs through continual post-training. While pre-training equips LLMs with broad linguistic knowledge, it often falls short in complex reasoning tasks like math or code. Recent models have shown that Reinforcement Learning with Verifiable Rewards (RLVR) can help bridge this gap, but existing methods rely on slow and limited online training. We propose an offline alternative using teacher-generated trajectories and introduce a novel variant of Group Relative Policy Optimization (GRPO) that better captures high-quality reasoning traces—even when all outputs are positive. Our experiments on mathematical reasoning show that this method leads to consistent improvements.
Beyond SOTA MATH LLMs: A Continual Post-training Method for State-of-the-Art (SOTA) LLMs in MATH.
We propose a continual post-training method that further enhances the mathematical reasoning performance of various Large Language Models (LLMs). Although online GRPO is a commonly used for post-training, it suffers from long training times and is constrained by the capabilities of the base LLM. To address these issues, we use an offline GRPO method, which learns from a pre-existing dataset of high-quality solutions generated by a more capable teacher model. Additionally, we introduce a bias term in the advantage function to ensure that all positive trajectories are effectively learned. As a result, we developed LLMs with specialized performance in mathematics, as illustrated in Figure 1. We also confirmed that this training method maintains the performance of the original model on tasks other than mathematics.
Why do we focus on post-training for reasoning?
The pre-training of LLMs on large text corpora plays a crucial role in capturing statistical patterns and language structures. However, this is often insufficient for tasks that require complex, multi-step logical reasoning, mathematical problem-solving, or code generation. For instance, while using Chain-of-Thought (CoT) can mimic the reasoning process to some extent, its performance is limited because the model has not fully internalized a coherent flow of reasoning.
Reinforcement Learning with Verifiable Rewards (RLVR) is designed to overcome these limitations. The effectiveness of this post-training approach in enhancing the reasoning capabilities of LLMs has gained prominence, with models like DeepSeek-R1 and OpenAI’s o1/o3 models demonstrating substantial improvements in reasoning performance via RLVR. RLVR requires the entire reasoning process generated by the LLM—a rollout trajectory in the form of Chain-of-Thought (CoT)—to be verifiable. For example, in a math problem with a known answer, the final solution can be directly compared, or each step can be evaluated, enabling reward assignment to the entire generated trajectory. Based on such rewards, RL algorithms (e.g., PPO, GRPO) are used to train the LLM to generate correct reasoning processes.
Group Relative Policy Optimization (GRPO)
where $\pi^{i,t} = \pi(o_{i,t}\mid q, o_{i,<t})$, and $G$ represents the number of responses in a group. Also, $\pi_{ref}$, $\pi_{\theta}$, and $\pi_{old}$ denote the reference LLM, the LLM being trained, and the LLM from the previous step used for sampling, respectively. $q$ and ${o_i}_{i=1}^{G}$ denote the set of questions and the generated rollout trajectories used for training. The relative advantage of each response $\hat{A}_i$ is calculated as follows:
\[\hat{A}_i = \frac{r_i - \text{mean}(r_i)}{\text{std}(r_i)}\]This trajectory-level advantage is then applied to each token level of the response, ultimately being used as $\hat{A}_{i,t}$.
Offline Reinforcement Learning with Verifiable Reward
Why do we focus on Offline RLVR (e.g., GRPO)?
The RLVR method described earlier computes the advantage in an online manner. This means that the LLM is updated based on the rewards of the rollout trajectories generated by itself.
However, online training has two main drawbacks.
The first is its slow training speed.
To overcome these drawbacks of online methods, we turn our attention to offline RLVR methods that utilize pre-existing rollout trajectories of teacher LLMs.
In this project, we use the OpenThoughts3
Denoting the teacher model $\theta_{teacher}$ and the random variable for the problems that the teacher has seen as $Q$, we can write the offline GRPO equation as follows:
\[\mathcal{L}_{Off-GRPO}(\theta) = \mathbb{E}_{[q \sim P(Q), \{o_i\}_{i=1}^{G}\sim \pi_{\theta_{teacher}}(O|q)]}\left[ \frac{1}{G}\sum_{i=1}^{G}\frac{1}{|o_i|}\sum_{t=1}^{|o_i|}\left\{ \min\left[\frac{\pi_{\theta}^{i,t}}{\pi_{\theta_{teacher}}^{i,t}}\hat{A}_{i,t},\text{clip}\left(\frac{\pi_{\theta}^{i,t}}{\pi_{\theta_{teacher}}^{i,t}},1-\epsilon,1+\epsilon\right)\hat{A}_{i,t}\right] -\beta\mathbb{D}_{KL}\left[\pi_{\theta}\mid\mid\pi_{ref}\right]\right\} \right]\]Since we do not know the likelihood of the trajectory under the teacher model in practice, we assume $\pi_{\theta_{teacher}}^{i,t} = 1$.
This means that $\frac{\pi_{\theta}^{i,t}}{\pi_{\theta_{teacher}}^{i,t}} \le 1$ is always true, $\text{clip}$ can be expressed as $\max\left(\pi_{\theta}^{i,t},1-\epsilon\right)$.
Therefore, the offline GRPO objective can be approximated as follows:
Offline GRPO vs. Supervised Fine-tuning (SFT)
The simplest way to train a model with offline data is SFT. So, what distinguishes SFT from offline GRPO? The difference becomes clear by comparing the SFT loss equation below with that of offline GRPO.
\[\mathcal{L}_{SFT}(\theta) = \mathbb{E}_{q \sim P(Q),\,o \sim \pi_{\theta_\text{teacher}}^{(+)}(O|q)}\left[\frac{1}{|o|}\sum_{t=1}^{|o|}\log\pi_{\theta}(o_{t}|q,o_{\lt t}) - \beta\mathbb{D}_{KL}\left[\pi_{\theta}\mid\mid\pi_\text{ref}\right]\right]\]Here, $\pi_{\theta_{teacher}}^{(+)}(O|q)$ indicates that only positive samples from the teacher’s generations are selected. This supervised learning loss guides the model to follow the distribution of only the positive samples.
When compared with our approximated offline GRPO loss equation, it can be seen that the offline GRPO also leverages negative samples. In Offline GRPO, the model learns to move toward positive samples and away from negative ones. This property strengthens the model’s reasoning ability by steering it away from logically incorrect rollout trajectories. We support this claim with the following experiment.
Let’s try out our experiment
We conducted an experiment to verify whether the offline GRPO method is more effective in enhancing reasoning ability than supervised fine-tuning (SFT), which only learns from positive samples. We used OpenThinker3-7B as our base model, and sampled approximately 2,000 Math problems from OpenThoughts3 as training data. The implementation was built on top of the VERL framework. For the training, we used a learning rate of 1e-7, a batch size of 32, 3 epochs, and a KL coefficient of 0.1. 8 samples were used per problem during training.
Using AIME24 as the validation set to measure performance at each epoch, the best-performing checkpoint across the three epochs was selected, and final performance was evaluated on AIME25-1 and AIME25-2. The experimental results are as follows:
| Method | AIME25-1 Score | AIME25-2 Score |
|---|---|---|
| Base model | 55.31 | 61.25 |
| SFT | 55.83 | 57.4 |
| Offline GRPO | 55.21 | 63.02 |
We show that Offline GRPO outperforms SFT by allowing the model to learn from negative samples as well. While all training data are treated as positive in SFT, we improve the supervised learning setup by incorporating more informative reward signals through majority voting and offline GRPO.
In this experiment, we have demonstrated the effectiveness of Offline GRPO in further enhancing the reasoning ability of existing SOTA LLMs. We believe such method has potential to be applied to various other domains that require reasoning in the future.
Proposed Loss for RLVR: Challenges & Solutions
Challenges: Considering all positive reasoning trace
A key issue arises when naively applying GRPO’s advantage calculation in the offline setting. When all rollout trajectories are positive and the mean reward is 1, the resulting advantage becomes 0. This means that no updates are made for those samples.
In the case of online GRPO, these all-positive samples are not problematic because the model is already performing well, making further learning from such easy problems unnecessary.
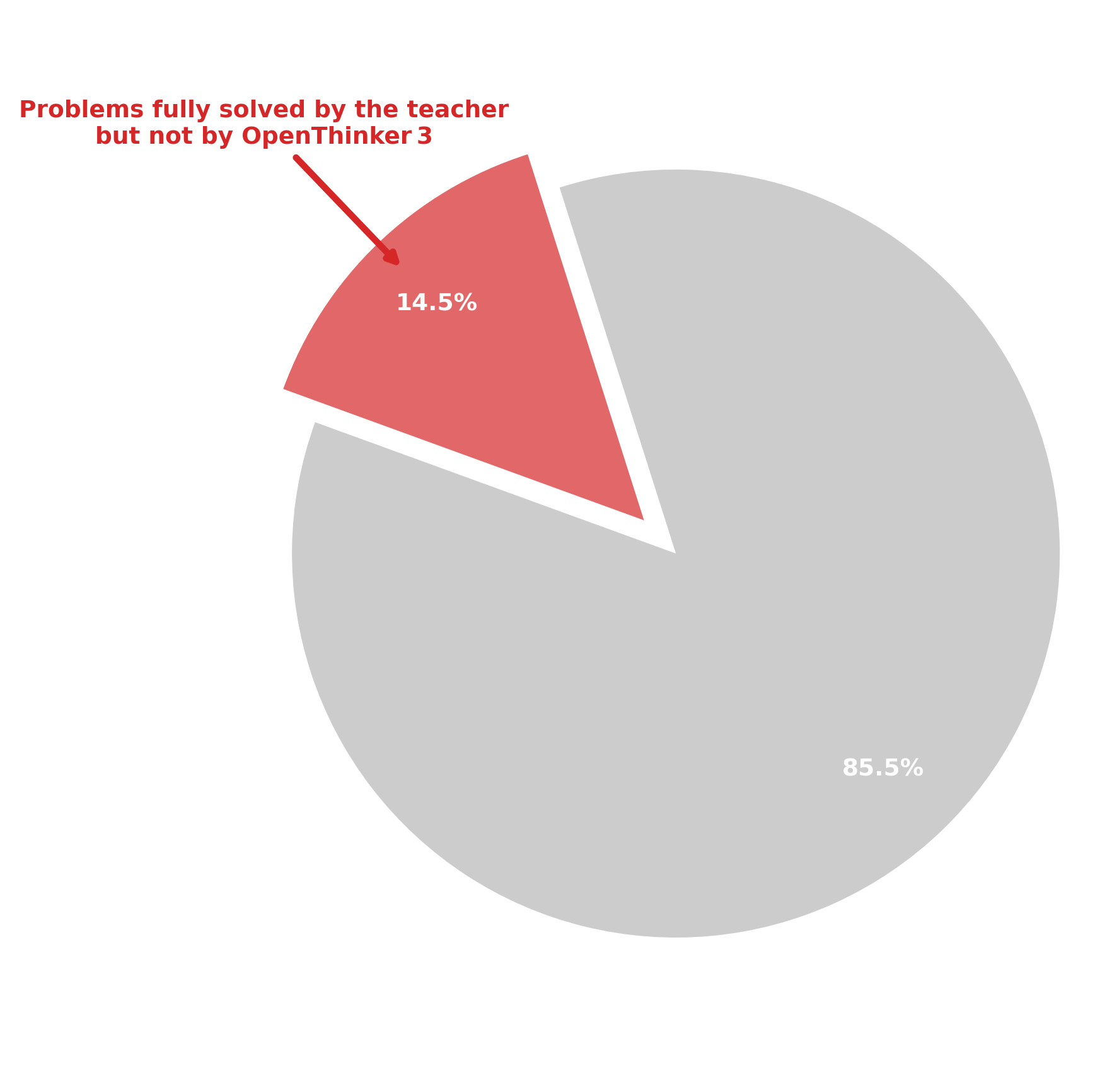
However, in the offline setting, ignoring all-positive samples can be detrimental. In our setup, the offline samples are sourced from a teacher model. Even if all teacher samples are positive, this does not necessarily mean the target model can solve the same problems perfectly. The current objective fails to capture this discrepancy, missing valuable learning opportunities from high-quality rollout trajectories.
The figure below shows this discrepancy in our dataset.
Proposed method
To address the issue described above, we propose a simple modification to the loss term by adding a bias term $b$ to the advantage when all rollout trajectories are positive. This ensures that updates are made even when all samples are positive, thus enabling learning from fully positive reasoning traces. Specifically, the modified loss equation is as follows:
\[\mathcal{L}_{ours}(\theta) = \begin{cases} \mathbb{E}\left[ \frac{1}{G} \sum\limits_{i=1}^{G} \frac{1}{|o_i|} \sum\limits_{t=1}^{|o_i|} \left\{ \min\left[\pi_{\theta}^{i,t}(\hat{A}_{i,t} + b), \max(\pi_{\theta}^{i,t}, 1-\epsilon)(\hat{A}_{i,t} + b)\right] - \beta \mathbb{D}_{KL}\left[\pi_{\theta} \,\|\, \pi_{ref} \right] \right\} \right] & \text{if all } r_{i} > 0 \\ \\ \mathbb{E}\left[ \frac{1}{G} \sum\limits_{i=1}^{G} \frac{1}{|o_i|} \sum\limits_{t=1}^{|o_i|} \left\{ \min\left[\pi_{\theta}^{i,t} \hat{A}_{i,t}, \max(\pi_{\theta}^{i,t}, 1-\epsilon)\hat{A}_{i,t}\right] - \beta \mathbb{D}_{KL}\left[\pi_{\theta} \,\|\, \pi_{ref} \right] \right\} \right] & \text{otherwise} \end{cases}\]For our experiments, we set $b=0.5$.
Let’s try out our experiment
In this experiment, we demonstrate that the proposed method improves performance over the existing offline GRPO.
We used the exact same experimental setup as in the first experiment, changing only the training objective. The same model (OpenThinker3-7B), the same data (2,000 math problems from OpenThoughts3), and the same hyperparameters (learning rate=1e-7, batch size=32, epochs=3, KL coefficient=0.1, 8 samples per problem) were used. The bias term was set to 0.5.
Performance was evaluated in the same manner—selecting the best checkpoint using AIME24 as the validation set and then evaluating final performance on AIME25-1 and AIME25-2. The experimental results are as follows:
| Method | AIME25-1 Score | AIME25-2 Score |
|---|---|---|
| Base model | 55.31 | 61.25 |
| Offline GRPO | 55.21 | 63.02 |
| Offline GRPO (with all positive group bias) | 56.35 | 63.85 |
The experimental results show that the proposed modified offline GRPO outperforms not only the base model but also the existing offline GRPO. We believe these improvements stem from effectively learning from cases where all teacher samples are positive, which were previously ignored.
In conclusion, we show that the proposed modified loss successfully addresses the limitation of existing offline GRPO in learning from all-positive samples, thereby further improving the model’s reasoning performance. We believe this modification can also be effective in domains beyond mathematics.
Generalization Across Multiple Models and Benchmarks
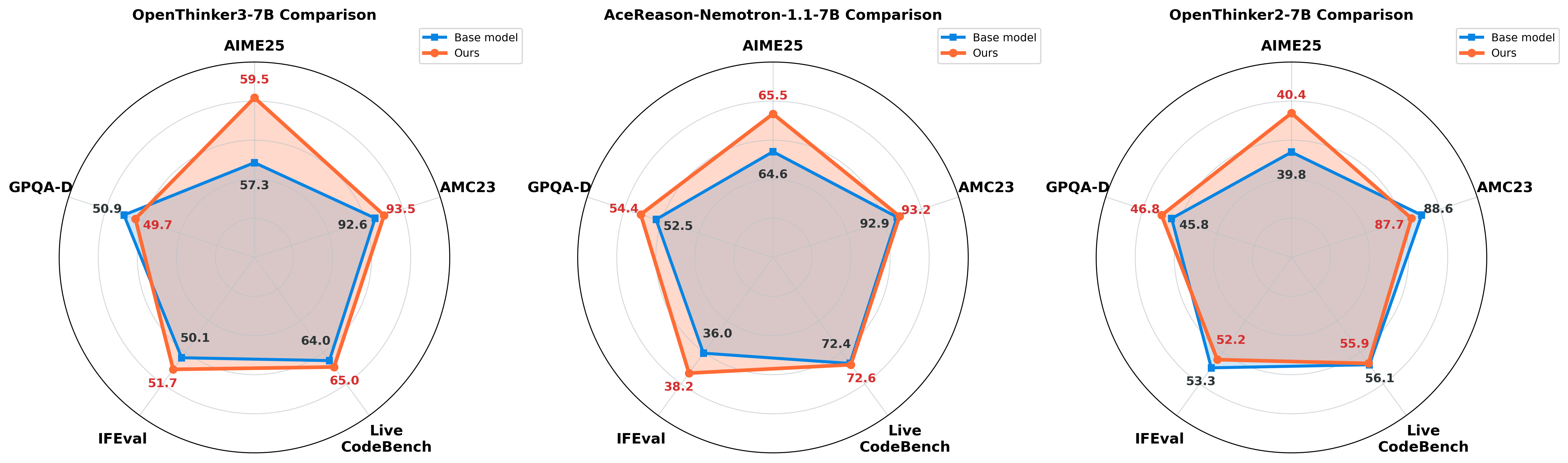
We further investigated whether our proposed continual post-training methodology consistently improves performance across a broader range of models and various benchmarks. To this end, we maintained the previous experimental setup and additionally evaluated two additional models: OpenThinker2-7B and AceReason-Nemetron-1.1-7B. We also extended our evaluation to a broader range of benchmarks: AIME25 and AMC23 for mathematical problem-solving skills, LiveCodeBench for code generation ability, GPQA-Diamond for general reasoning ability, and IFEval for instruction-following. We used the SkyThought framework for AIME25, AMC23, LiveCodeBench, and GPQA-Diamond, and the llm-evaluation-harness for IFEval.
The experimental results are presented in the table below:
| Model | Method | AIME25 | AMC23 | LiveCodeBench | GPQA-Diamond | IFEval |
|---|---|---|---|---|---|---|
| Openthinker3-7B | Base | 57.292 | 92.617 | 63.968 | 50.947 | 50.09 |
| Offline GRPO (+bias) | 59.532 | 93.516 | 64.995 | 49.684 | 51.66 | |
| Openthinker2-7B | Base | 39.792 | 88.633 | 56.115 | 45.833 | 53.30 |
| Offline GRPO (+bias) | 40.365 | 87.656 | 55.944 | 46.843 | 52.20 | |
| AceReason-Nemetron-1.1-7B | Base | 64.635 | 92.930 | 72.383 | 52.462 | 36.02 |
| Offline GRPO (+bias) | 65.521 | 93.164 | 72.603 | 54.356 | 38.23 |
As the models were post-trained on math data, all models showed consistent performance improvements on the math-related benchmarks (AIME25, AMC23). Interestingly, performance in other domains was maintained without degradation compared to the original models, and even showed a slight improvement on the code generation benchmark, LiveCodeBench. These results indicate an absence of any catastrophic forgetting during the continual post-training process.
Additionally, offline GRPO is highly efficient as it recycles the teacher model’s trajectories without direct rollout during the training process. We therefore achieved performance comparable to or better than existing reinforcement learning methods while significantly reducing computational cost. Being compute-efficient yet strong in performance, we believe that our proposed continual post-training methodology is attractive to many practitioners, and expect it to be useful across various domains and applications. Finally, we have publicly released all the evaluated models on HuggingFace to contribute to the open-source community and to make our results reproducible.